Parallel and High-Performance Computing
The research focuses on algorithms, tools, and applications for scalable high-performance computer systems and the important issue of the scalability of a parallel algorithms (or applications).
Current research topics include
- high-performance and portable linear algebra kernels,
- direct and iterative methods for linear systems and eigenvalue problems,
- development tools for parallel computing , and parallel algorithms in optimization.
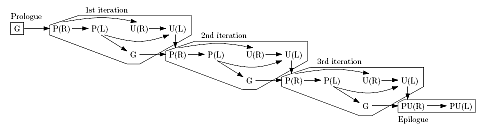
Hierarchically Blocked Algorithms and Optimized Kernels for Dense Matrix Computations on Memory-Tiered High-Performance Computing Systems
Focus on developing new theory, methods, and algorithms to produce high-quality, reusable software that deliver close to practical peak performance on today`s evolving deep memory HPC multicore architectures. This also includes development of software tools and environments for design of parallel algorithms and applications. The research group participates in international collaboration regarding high-performance software libraries (e.g., LAPACK, ScaLAPACK, SLICOT).
The research program subject include:
- Square and Recursive Blocked Algorithms and Hybrid Data Structures for Matrix Computations.
- Blocked and Parallel Matrix Equation Solvers.
- Blocked and Parallel Two-sided Reductions to Condensed Forms.
- Blocked and Parallel Reduction to Schur Forms.
- HPC Software and Tools. The deliverables also include an essential set of high-performance software and tools in support for scientists and engineers to enable their applications.