Efficient and Reliable HPC Algorithms for Matrix Computations in Applications
Parallelism is here to stay! Today, most computers, from laptops to supercomputers, are based on the so-called multicore architectures. Connecting many thousands of powerful, and possibly heterogeneous, multicore and accelerator based nodes using a high-performance interconnect leads to truly massive parallel systems with a tremendous performance potential. A state-of-the-art resource for the Swedish e-Science is the Kebnekaise system at HPC2N, which in addition to multi-core compute nodes, includes extremely large memory nodes (3TB per node) and nodes with accelerators (Nvidia GPU and Intel KNLs). This evolution makes it possible to solve even more complex and large-scale computational problems in science and engineering. At the same time, there is an immense demand for new and improved scalable, efficient, and reliable numerical algorithms, library software, and tools. This is essential, so that computations are carried out in a reasonable time and with the accuracy and resolution required.

Matrix computations are both fundamental and ubiquitous in the Computational Sciences, for example, in the modelling and simulation of problems ranging from galaxies to nanoscale, and in real-time airline scheduling and medical imaging. Computing the Google PageRank vector of all web pages on the Internet is called the world´s largest matrix computation of today, with a hyperlink matrix of n-by-n, where n > 50 billion.
Besides such large-scale problems, there are many challenging matrix computations in the design and analysis of linear control systems. Modeling interconnected systems (electrical circuits, for example) and mechanical systems (such as multibody contact problems) can lead to descriptor systems. Periodic models arise in several practical applications, e.g., the control of rotating machinery. We are investigating how to exploit the inherent structure of several of the associated matrix problems.
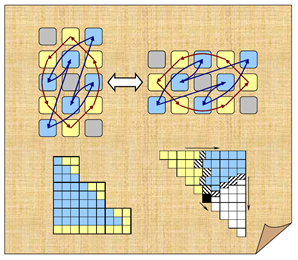
Aims and research focus
In this project, we develop generic methods and tools for various matrix computations in e-Science, spanning the whole spectrum from small- to very large-scale problems. Everything from core problems in linear algebra to matrix equations and eigenvalue problems appearing in various applications are addressed. To achieve the best performance and maximize the utilization of today’s and future large-scale HPC systems, the algorithms and data structures must match the hardware, including deep memory hierarchies, as well as the functionality of the compilers.
Examples of problems addressed:
- Design of parallel and cache-efficient algorithms and matrix data structures for multi-core and hybrid architectures.
- Development of robust and efficient parallel solvers for both standard and generalized dense and non-symmetric eigenvalue problems.
- Algorithms for solving nonlinear constraint equations in the context of molecular dynamics, which are not only robust, but more accurate and much faster than previous solvers.
- Auto-tuning of software parameters, compiler flags, or even selecting the best kernel from a set of kernels. Among the approaches are off-line and on-line tuning.
- Study on how canonical forms behave under small perturbations and reveal the qualitative information that the closure hierarchy of orbits and bundles provide.
- Development of robust methods for computing the canonical structure information for matrices, matrix pencils, and matrix polynomials.
The results include novel theory, algorithms, library software, and tools to be used as building blocks for various academic and industrial applications.
International awards and research grants
Research conducted in this project, made possible via grants from the Strategic Program eSSENCE and the Swedish Research Council (VR), has been rewarded internationally:
- Andrii Dmytryshyn awarded SIAM Student Paper Prize 2015.
- Bo Kågström appointed SIAM Fellow 2016.
- The Research and Innovation project NLAFET, acronym for Parallel Numerical Linear Algebra for Future Extreme Scale Systems, has been awarded with nearly 4 million Euros (over three years) by the European Commission within the Future and Emerging Technologies (FET) HPC program under Horizon 2020.
Research group
PI: Prof. Bo Kågström
Dept of Computing Science and HPC2N, Umeå University
Dr. Andrii Dmytryshyn, Dr. Stefan Johansson, Asst. prof. Lars Karlsson, Dr. Carl Christian Kjelgaard Mikkelsen, and Dr. Mirko Myllykoski
Dept of Computing Science, Umeå University
Björn Adlerborn, Mahmoud Eljammaly, and Angelika Schwarz
Dept of Computing Science, Umeå University
Links and references
NLAFET, http://www.nlafet.eu/
StratiGraph and the MCS Toolbox for Matlab, http://www.cs.umu.se/english/research/groups/matrix-computations/stratigraph
Selected publications:
- Björn Adlerborn, Bo Kågström, and Daniel Kressner, A Parallel QZ Algorithm for Distributed Memory HPC Systems. SIAM J. Sci. Comput., 36(5):C480-C503, 2014.
- Andrii Dmytryshyn, Stefan Johansson, and Bo Kågström, Canonical Structure Transitions of Systems pencil. Preprint report UMINF 15.15, submitted 2016.
- Andrii Dmytryshyn and Bo Kågström, Orbit closure hierarchies of skew-symmetric matrix pencils. SIAM J. Matrix Anal. Appl., 35(4), 1429-1443, 2014.
- Andrii Dmytryshyn and Bo Kågström, Coupled Sylvester-type matrix equations and block diagonalization. SIAM J. Matrix Anal. Appl., 36(2), 580-593, 2015. (Awarded SIAM Student Paper Prize 2015)
- Robert Granat, Bo Kågström, Daniel Kressner, and Meiyue Shao, ALGORITHM 953: Parallel Library Software for the Multishift QR Algorithm with Aggressive Early Deflation. ACM Trans. Math. Software, Vol. 41; Issue 4, 29:1-29:22, 2015.
- Fred Gustavson, Lars Karlsson, and Bo Kågström, Parallel and Cache-Efficient In-Place Matrix Storage Format Conversion . ACM Trans. on Math. Software, Vol. 38, 17:1-17:32, 2012.
- Stefan Johansson, Bo Kågström, and Paul Van Dooren, Stratification of full rank polynomial matrices. Linear Algebra and its Applications, 439(4), 1062-1090, 2013.
- Lars Karlsson, Carl Christian Kjelgaard Mikkelsen, and Bo Kågström, Improving Perfect Parallelism. Parallel Processing and Applied Mathematics, PPAM 2013, Part I, LNCS vol. 8384, pp. 76-85, Springer 2014.
- Lars Karlsson, Bo Kågström, and Eddie Wadbro, Fine-Grained Bulge-Chasing Kernels for Strongly Scalable Parallel QR Algorithms. Parallel Computing, 40:271-288, 2014.
- Lars Karlsson, Daniel Kressner, and Bruno Lang, Optimally Packed Chains of Bulges in Multishift QR Algorithms. ACM Trans. Math. Software, 40(2)Article 12:1-15, 2014.
- Lars Karlsson, Daniel Kressner, and André Uschmajew, Parallel Algorithms for Tensor Completion in the CP Format. Parallel Computing, Vol. 57:C:222-234, September 2016.
- Lars Karlsson and Francoise Tisseur, Algorithms for Hessenberg-Triangular Reduction of Fiedler Linearization of Matrix Polynomials. SIAM J. Sci. Comput., 37(3), C384-C414, 2015.
- Carl Christian Kjelgaard Mikkelsen, Jesús Alastruey-Benedé, Pablo Ibáñez-Marín, Pablo García Risueño:, Accelerating Sparse Matrix Arithmetic in the context of Newton’s method for Small Molecules with Bond Constraint. 11th Int. Conference Proceedings of the Parallel Processing and Applied Mathematics (PPAM), 2015.
Theses:
- Björn Adlerborn, Parallel Algorithms and Library Software for the Generalized Eigenvalue Problem on Distributed Memory Computer Systems. PhLicentiate Thesis, Department of Computing Science, Umeå University, Report UMINF 16.11, May 2016.
- Andrii Dmytryshyn, Tools for Structured Matrix Computations: Stratifications and Coupled Sylvester Equations. PhD Thesis, Department of Computing Science, Umeå University, Report UMINF 15.18, December 2015.
- Meiyue Shao, Dense and Structured Matrix Computations – the Parallel QR Algorithm and Matrix Exponentials. PhD Thesis EPFL, 2014 (co-supervised with Daniel Kressner).