Parallelization of dynamic algorithms
Parallel computing is more important than ever before. To make best use of the computational power available today it is in general necessary that your program runs in parallel. There is a great and growing demand for easy-to-use programming models for parallel and high performance computing. The de facto standard for distributed computing, the message passing interface (MPI), is more than 20 years old and although the interface has been upgraded the fundamental programming model remains essentially unchanged. Development of applications within the message passing parallel programming paradigm is difficult and costly. In particular, parallelization of dynamic algorithms, with a priori unknown and/or dynamically changing distributions of work and data, often represents a formidable challenge. At the same time, many problems are such that dynamic algorithms would be the natural and appropriate choice if only suitable parallelization tools were available. This project targets the development of parallelization strategies (programming models, interfaces, and tools) for dynamic algorithms.
Aims
Our main goal is to greatly simplify the development and maintenance of parallel programs. We propose and develop a new programming model called Chunks and Tasks. Our anticipation is that the simplicity of our programming model will 1) lower the threshold to at all parallelize software and 2) greatly reduce development and maintenance costs for parallel software. The characteristics of our model will also 3) lead to less data movement and communication and thus improved performance and 4) allow for resilience to failures without need for intervention from the application programmer.
We target in particular applications with dynamic work and data in the sense that the best or any good distribution of work and data is not known in advance and may change dynamically during the calculation.
Methods
The application programmer exposes parallelism to the runtime library by writing her program as trees of tasks. Large data is stored as chunk trees generated by the execution of task trees.
Key features of the Chunks and Tasks programming model are: 1) The application programmer is responsible for exposing parallelism to the runtime library but not for the mapping of work and data to physical resources. 2) The Chunks and Tasks model provides abstractions for both work and data. 3) No explicit communication calls in user code. 4) Determinism, freedom from race conditions and deadlocks. 5) Feasible to implement efficient backends. 6) Fail safety: local recovery possible without intervention of the application programmer.
IMPLEMENTATION:
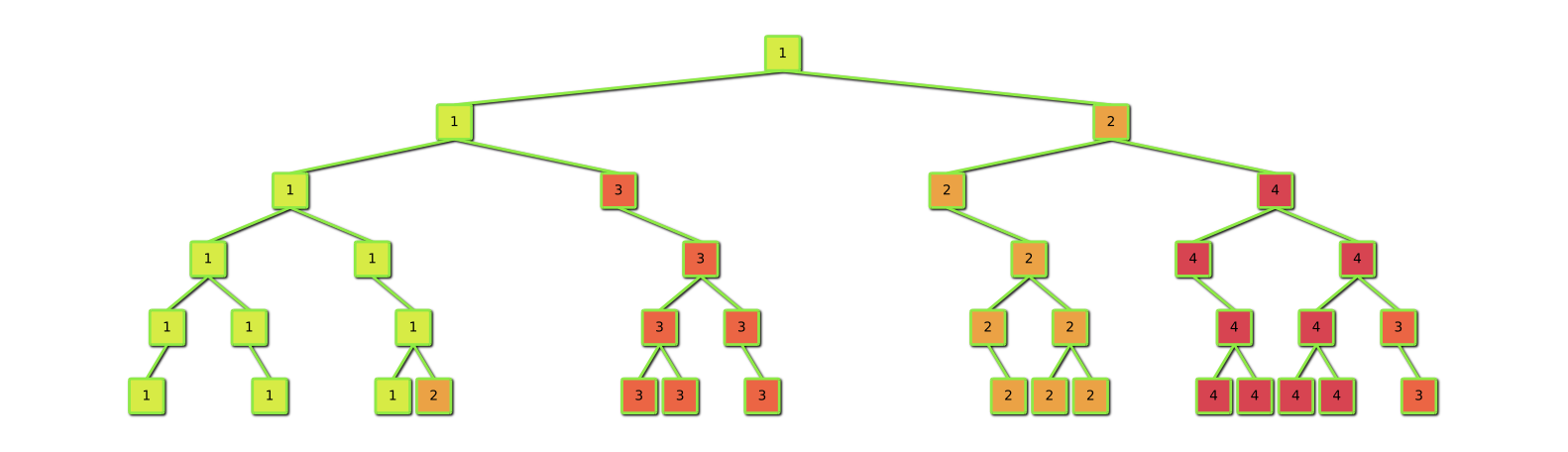
Our first Chunks and Tasks implementation is built on top of MPI and pthreads. Tasks are distributed using work stealing: One process starts to execute the mother task. Idle processors randomly select a victim process and steal tasks as high up as possible in the task tree of the victim. The figure illustrates a possible distribution of tasks between four processors (numbered 1-4 in the figure) for a sparse binary tree of tasks. Chunks of data resulting from task execution are by default stored at the process executing the task. Chunks needed for task execution can readily be fetched from their owners since the chunk location is stored in the identifier of the chunk. Recently used chunks are cached for efficient reuse of already fetched data.
Research group
PI:Emanuel H. Rubensson (Associate Professor, Docent)
Dept. of Information Technology, Uppsala University
PI: Elias Rudberg (Researcher)
Dept. of Information Technology, Uppsala University
Anastasia Kruchinina (PhD Student), Dept. of Information Technology, Uppsala University
Anton Artemov (PhD Student), Dept. of Information Technology, Uppsala University
Links and references
Chunks and Tasks: A programming model for parallelization of dynamic algorithms,
Emanuel H. Rubensson and Elias Rudberg, Parallel Comput. 40, 328 (2014)
Locality-aware parallel block-sparse matrix-matrix multiplication using the Chunks and Tasks programming model, Emanuel H. Rubensson and Elias Rudberg, Parallel Comput. 57, 87 (2016).