A unified theory of the rare-earth elements

A unified theory of the rare-earth elements

Rare-earth elements are found in a wide range of functional materials, with diverse applications. They are fundamental components of the most used permanent magnets and can also be found in materials showing multiferroism [1]. Furthermore, rare-earth impurities in semiconductors are frequently used in optical fibers for signal enhancement, in high-power fiber lasers, as well as in photovoltaic applications. Examples can also be found of rare-earth containing compounds with topologically protected surface states, e.g. in the mixed valence semiconductor SmB₆. Moreover, there is recent interest in rare-earth elements in molecular magnets, e.g. in so called phthalocyanine double-deckers. These examples illustrate the relevance of the rare-earth elements in various research fields, ranging from applied technology to more fundamental aspects of the electronic structure of solids. In this context, it is very limiting that there exist no theory offering a good description of the electronic and magnetic properties of rare-earth elements and compounds. Developing such a theory is the aim of this project.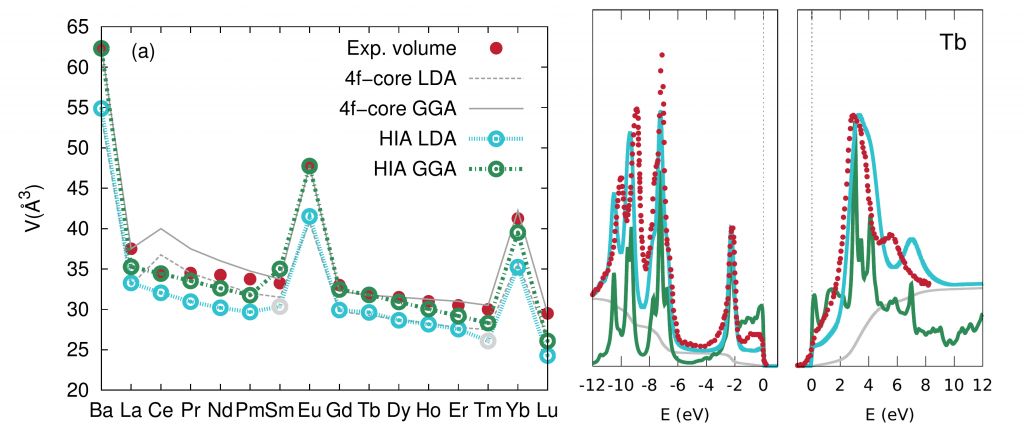

Aims
In this project we aim to develop a unified computational scheme to describe all major properties of the rare-earth elements. Our method of choice is the combination of density functional theory (DFT) and dynamical mean-field theory (DMFT) in the Hubbard I approximation (HIA) [2]. We have already applied this approach to describe the cohesive properties of the whole series of the rare-earth elements, as illustrated in Figure 1 (equilibrium atomic volume across the series) [3]. As this plot shows, our approach reproduces the experimental values to a good accuracy. Even better accuracy is reached for the spectral properties, as illustrated in Figure 2 for elemental Tb (the red dots correspond to direct and inverse photoemission data, while the green and blue curves to the bare HIA spectral function, respectively without and with background emission) [3].
While this computational scheme is very efficient to describe the properties of a paramagnetic system, methodological problems arise when addressing the ferromagnetic state, as well as any other symmetry-broken state. This is a severe limitation when studying rare-earth compounds, since magnetic properties are of primary interest, especially in relation to the magnetic anisotropy. We are now working to solve technical problems related to the inclusion of magnetic exchange, crystal field splitting and non-spherical contributions to the electronic potential in the DFT+DMFT approach. We will then apply the developed technique to study magnetism and crystal-field levels splitting in the whole series of rare-earth elements.

Methods
This project is based on the combination of DFT and DMFT, as implemented in the electronic structure code RSPt [4]. The latter is based on the full-potential linear muffin-tin orbital (FP-LMTO) method and is particularly efficient for DMFT calculations, due to the small number of basis functions. The HIA consists in approximating the impurity problem arising in DMFT with an atomic-like problem [3]. This approximation is very good for all rare-earth elements, with the exception of Ce, for which some discrepancies are expected.

Research group

PI:Prof. Olle Eriksson
Dept of Physics and Astronomy, Uppsala University
Igor Di Marco, Project leader
Dept of Physics and Astronomy, Uppsala University
Inka L. M. Locht
Dept of Physics and Astronomy, Uppsala University
L. V. Pourovskii
de Physique Théorique (CPHT), École Polytechnique, Palaiseau Cedex, France

Links and references